Lidé, přesněji investoři, si často kladou otázky ohledně bankovních vkladů nebo investičních fondů a přesného výpočtu jejich zisku či úroků. Finačné společnosti často zveřejňují výnosy na víceleté období - například 5-leté, což je však zkreslující údaj a není srovnatelný například s úrokem v bankách při vkladu na 5 let (ty jsou zveřejněny per annum). Základními problémy, s nimiž se investoři potýkají jsou následující:
- Celková uspořená částka při jednorázovém vkladu
- Celková uspořená částka při pravidelných a rovnoměrných vkladech - anuita (např. při spoření na konkrétní účel v budoucnosti)
- Celková uspořená částka při nepravidelných a nerovnoměrných vkladech (když budu mít peníze, tak si něco odložím, když ne, tak neodložím nic)
- Výpočet úroku
Jsou to časté otázky a nejen v souvislosti se spořením na důchod. Představte si, že se živíte např. obchodováním komodit, Forexu, nebo obecněji futures trhů a pravidelně, nebo nepravidelně si chcete odkládat část svého výdělku bokem. Někdy odložíte 100 Eur, někdy 1000 Eur a někdy pár měsíců nemusíte odložit ani jediné Euro. Právě pro takové případy investorům přiblížíme princip výpočtu zisku a úroku různých forem spoření.
Jednorázový vklad
Základním a zároveň nejjednodušší formou spoření je jednorázový vklad. Když máte k dispozici částku, kterou si chcete uložit, výpočet je jednoduchý. Vzorec vypadá následovně
BH = SH x [(1 + i) na n]
SH = původní vklad
i = úroková míra
n = počet let
Jinými slovy, to, kolik budete mít v budoucnu naspořeno, vypočítáte, když svůj vklad vynásobíte: (1 + úrok) umocněno na počet let, na který budete mít částku uloženou v bance. Tento výraz se nazývá úročiteľ.
Příklad:
Chcete investovat 10 000 Eur na 6 let. Banka nabízí úrok 5%. Po dosazení do vzorce je to:
BH = 10 000 x [(1 + 0,05) na 6]
BH = 13 401 Eur
Pokud bychom vklad vložili jednorázově do banky, mohli bychom vydělat 3 401 Eur navíc na úrocích.
Pravidelný a rovnoměrný vklad - Anuita
Pravidelný a rovnoměrný vklad se jmenuje anuita. Klasickým příkladem je např. situace, kdy si z každé výplaty odložíte 100 Eur na svůj budoucí důchod. Kromě částky potřebujete vědět také úrok, kterým máte vklad úročen a počet let, jak dlouho si budete spořit. Pokud vkládáte vícekrát do roka, tak i počet vkladů. Pak je již výpočet jednoduchý. V našem případě:
BH = anuita x [((1 + i/m) na n*m) / (i/m)]
anuita = pravidelný a stejný vklad
i = úroková míra
n = počet let
m = počet vkladů v roce (při vkladu každý měsíc je to 12)
Příklad:
Každý měsíc si odkládáte anuitu 100 Eur. Odkládat si takto plánujete 30 let a úrok, který nabízí banka je 3%. Tím, že investujete každý měsíc a ne pouze 1x ročně, je zde nutné započítat nový faktor - m (počet období v roce, kdy tak učiníte).
BH = 100 x [((1 + 0,03/12) na 30*12) / (0,03/12)]
BH = 58 274 Eur
Celkově jste si odložili 100 Eur * 30 let * 12 měsíců = 36 000 Eur. Naspořených je 58 274 Eur. Na úrocích jste vydělali 22 274 Eur.
O situaci, že byste potřebovali například vypočíst skutečný úrok ze své pravidelné investice do podílových fondů jsme se už bavili v tomto článku.
Nepravidelný a nerovnoměrný vklad
Doposud uvedené výpočty byly jednoduché. Nepravidelné a nerovnoměrné vklady jsou však specifická situace. Neřeší to ani takový skvělý nástroj, jak je Excel. Vyžaduje se podstatně více znalostí a logického myšlení, abyste přišli na řešení. Kromě úroku potřebujete vědět přesné termíny a částky - kdy a kolik jste vložili. Pro výpočet lze použít první uvedený vzorec - úročiteľ, ale pro každý vklad s osobitou dobou pro úročení.
Příklad:
Peníze jsme vložili celkem 3krát:
12. ledna 2001 - 1260 €
27. května 2006 - 980 €
13. prosince 2008 - 1780 €
Data a částky byly vybrány čistě náhodně. Částky již známe, důležité je vypočítat počet let, kolik se každá uvedená částka bude úročit. Pokud bychom chtěli vypočíst hodnotu vkladů k dnešnímu dni (9. června 2012):
- první vklad (1260 €) by byl úročen 11,41 roku
- druhý vklad (980 €) by byl úročen 6,03 roku
- třetí vklad (1780 €) 3,49 roku.
Tyto zlomky roku dokáže vypočíst např. Excel, nebo si sami vypočtete počet dní mezi vkladem a dneškem a vydělíte jej číslem 365. Např. počet dní mezi 12. lednem 2001 a 9. červnem 2012 je 4166 dnů / 365 = 11,41 roku.
Pokud by byl úrok např. 5%, pak víme, že:
- první vklad bude úročen po dobu 11,41 let, při 5 %, t.j.:
BH = 1260 x [(1 + 0,05) na 11,41]
BH = 2199 €
- druhý vklad bude úročen po dobu 6,03 roku:
BH = 980 x [(1 + 0,05) na 6,03]
BH = 1315 €
- třetí vklad bude úročen 3,49 roku:
BH = 1780 x [(1 + 0,05) na 3,49]
BH = 2110 €
Celkem = 2199 + 1315 + 2110 = 5624 €
Do banky byste vložili celkově 4020 € a vybrali 5624 €. Zisk na úrocích je 1604 €.
Výpočet úrokové sazby u nepravidelných a nerovnoměrných vkladů.
S posledním uvedeným typem spoření souvisí jeden zajímavý problém - jak určit výši úrokové sazby, o kterou jsme zhodnotili naše peníze, pokud jsme vkládali nepravidelné nebo finančně nerovnoměrné vklady.
Pokud by byly vklady pravidelné - např. vždy 15. dne v měsíci, a rovnoměrné - např. vždy po 100 Eur, určit úrok by bylo poměrně jednoduché (MS Excel). Při nepravidelných a nerovnoměrných vkladech však selhává i ten.
Na ukázku použijeme předchozí příklad, který jsme řešili. Budeme vědět, kdy a kolik jsme vkládali a také to, kolik máme dnes v bance našetřeno (5624 €). Chceme vědět, kolik nám naše vklady skutečně vydělali v procentech.
O našich dosavadních vkladech máme tyto informace:
[1260 x [(1 + i) na 11,41]] + [980 x [(1 + i) na 6,03]] + [1780 x [(1 + i) na 3,49]] = 5624 €
i - (úroková míra) je v tomto případě neznámou
všechny ostatní faktory jsou pro nás známé - kolik jsme vložili, jak dlouho byly peníze vloženy, kolik je dnes našetřeno.
Na to, abychom vypočítali neznámou "i", použijeme Excel.
1. Do políčka A1 vložíme libovolnou úrokovou míru - např. 2%. A1 se bude snadno pamatovat, jak buňka, ve které hledáme skutečný úrok, který jsme vydělali.
2. Vedle - do sloupce B dáme pod sebe jednotlivé vklady, v našem případě
B1 = 1260 €
B2 = 980 €
B3 = 1780 €
3. Do sloupce C vložíme období, během kterého se budou jednotlivé vklady úročit:
C1 = 11,41
C2 = 6,03
C3 = 3,49
4. Do sloupce D vložíme vzorec, který je uveden výše. Ten rozložíme na příslušný počet částí (v našem případě 3). Sloupec D bude tedy vypadat následovně:
D1 = 1260 x (1 + i) na 11,41
D2 = 980 x (1 + i) na 6,03
D3 = 1780 x (1 + i) na 3,49
Jelikož my už máme uvedené hodnoty v Excelu napsáno, můžeme je do vzorce dosadit. Neznámou "i" nahradíme buňkou A1 (v této buňce budeme hledat řešení, zatím jsou tam 2%). Vypadalo by to následovně:
D1 = B1 x (1 + A1) na C1
D2 = B2 x (1 + A1) na C2
D3 = B3 x (1 + A1) na C3
Takto můžeme v Excelu spočítat, kolik bychom dnes měli, kdybychom vkládali konkrétné 3 částky na daný počet let, při předvolené úrokové míře 2% (buňka A1). V tomto případě bychom měli 4591 €. My ale víme, že na účtu je dnes 5624 €, t.j. podstatně více.
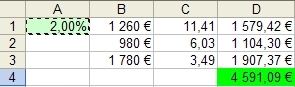
Prvním řešením je postupné ruční přepisování buňky A1, dokud nám suma všech vkladů (D4) nebude dávat jejich skutečnou současnou hodnotu 5624 €.
Druhou možností je využít v Excelu funkci "hledání řešení". Nachází se pod záložkou Nástroje. Podstata této funkce je v tom, že konkrétní buňku přepisuje, dokud se jiná buňka nerovná námi definované konečné hodnotě. Funkce vyžaduje určení 3 parametrů. V našem případě:
- nastavit buňku: "D4"
skutečně našetřeno suma všech vkladů, momentálně je tam při úrokové míře 2% částka 4591 €
- cílová hodnota: "5624"
protože víme, že je to částka, kterou máme na účtu a vydělali jsme tedy více, než zatím uvedeny 2%
- měněna hodnota: "A1"
procenta, které bude Excel měnit, dokud se buňka "D4" nebude rovnat "5624".

Stačí stisknout tlačítko OK a můžete sledovat, jak v průběhu sekundy Excel vypočítá, a do buňky A1 uvede, správné řešení. V našem případě se v buňce A1 ocitne hodnota 5%. Při 5% se totiž výsledná hodnota našich vkladů rovná přesně 5624 Eur, které máme na účtu dnes.
Následně se s takovým souborem můžete libovolně pohrát a sledovat, jak se mění výše úrokové sazby, při měnící se našetřené částce. Pokud bychom na našem účtu měli momentálně např. 10 000 €, vypočteme, že zhodnocení vkladů, které jsme našimi investicemi dosáhli by bylo 13,20%.
Excel umožňuje tyto výpočty ještě více zjednodušit - např. nemusíme sami určit, kolik let se každý vklad bude individuálně úročit, ale program sám dokáže vypočíst rozdíl mezi datem vkladu a dnešním (nebo libovolným jiným) datem. To však již není přímo obsahem tohoto článku. Cílem bylo přinést investorům řešení základního problému - jak lze vypočíst skutečné zhodnocení investovaných peněz.
