Ľudia, presnejšie investori, si často kladú otázky ohľadom bankových vkladov alebo investičných fondov a presného výpočtu ich zisku či úrokov. Finačné spoločnosti často zverejňujú výnosy na viacročné obdobia - napríklad 5-ročné, čo je však skresľujúci údaj a nie je porovnateľný napríklad s úrokom v bankách pri vklade na 5 rokov (tie sú zverejnené per annum). Základnými problémami, s ktorými sa investori potýkajú sú tieto:
- Nasporená suma pri jednorázovom vklade
- Nasporená suma pri pravidelných a rovnomerných vkladoch - anuita (napr. pri sporení na konkrétny účel v budúcnosti)
- Nasporená suma pri nepravidelných a nerovnomerných vkladoch (keď budem mať peniaze, tak si niečo odložím, keď nie, tak neodložím nič)
- Výpočet úroku
Jednorázový vklad
Základnou a zároveň najjednoduchšou formou sporenia je jednorázový vklad. Keď máte k dispozícii sumu, ktorú si chcete uložiť, výpočet je jednoduchý. Vzorec vyzerá nasledovne
BH = SH x [(1 + i) na n]
SH = pôvodný vklad
i = úroková miera
n = počet rokov
Inými slovami, to, koľko budete mať v budúcnosti nasporené, vypočítate, aj svoj vklad vynásobíte: (1 + úrok) umocnené na počet rokov, na ktorý budete mať sumu uloženú v banke. Tento výraz sa nazýva úročiteľ.
Príklad:
Chcete investovať 10 000 Eur na 6 rokov. Banka núka úrok 5 %. Po dosadení do vzorca je to:
BH = 10 000 x [(1 + 0,05) na 6]
BH = 13 401 Eur
Ak by sme vklad vložili jednorázovo do banky, mohli by sme zarobiť 3 401 Eur navyše na úrokoch.
Pravidelný a rovnomerný vklad - Anuita
Pravidelný a rovnomerný vklad sa volá anuita. Klasickým príkladom je napr. situácia, kedy si z každej výplaty odložíte 100 Eur na svoj budúci dôchodok. Okrem sumy potrebujete vedieť tiež úrok, ktorým máte vklad úročený a počet rokov, ako dlho si budete sporiť. Ak vkladáte viackrát do roka, tak i počet vkladov. Potom je už výpočet jednoduchý. V našom prípade:
BH = anuita x [((1 + i/m) na n*m) / (i/m)]
anuita = pravidelný a rovnaký vklad
i = úroková miera
n = počet rokov
m = počet vkladov v roku (pri vklade každý mesiac je to 12)
Príklad:
Každý mesiac si odkladáte anuitu 100 Eur. Odkladať si takto plánujete 30 rokov a úrok, ktorý ponúka banka je 3 %. Tým, že investujete každý mesiac a nie iba 1x ročne, je tu nutné zarátať nový faktor – m (počet období v roku, kedy tak učiníte).
BH = 100 x [((1 + 0,03/12) na 30*12) / (0,03/12)]
BH = 58 274 Eur
Celkovo ste si odložili 100 Eur * 30 rokov * 12 mesiacov = 36 000 Eur. Nasporených je 58 274 Eur. Na úrokoch ste zarobili 22 274 Eur.
O situácii, že by ste potrebovali napríklad vypočítať skutočný úrok zo svojej pravidelnej investície do podielových fondov sme sa už bavili v tomto článku.
Nepravidelný a nerovnomerný vklad
Doposiaľ uvedené výpočty boli jednoduché. Nepravidelné a nerovnomerné vklady sú však špecifická situácia. Nerieši to ani taký skvelý nástroj, ako je Excel. Vyžaduje sa podstatne viac vedomostí a logického zmýšľania, aby ste prišli na riešenie. Okrem úroku potrebujete vedieť presné dátumy a sumy – kedy a koľko ste vložili. Na výpočet sa dá použiť prvý uvedený vzorec – úročiteľ, ale pre každý vklad s osobitou dobou pre úročenie.
Príklad:
Peniaze sme vložili celkom 3-krát:
12. januára 2001 – 1260 €
27. mája 2006 – 980 €
13. decembra 2008 – 1780 €
Dátumy a sumy boli vybrané čisto náhodne. Sumy už poznáme, dôležité je vypočítať počet rokov, koľko sa každá uvedená suma bude úročiť. Ak by sme chceli vypočítať hodnotu vkladov k dnešnému dňu (9. júna 2012):
- prvý vklad (1260 €) by bol úročený 11,41 roku
- druhý vklad (980 €) by bol úročený 6,03 roku
- tretí vklad (1780 €) 3,49 roku.
Tieto zlomky roku dokáže vypočítať napr. Excel, alebo si sami vypočítate počet dní medzi vkladom a dneškom a vydelíte ho číslom 365. Napr. počet dní medzi 12. januárom 2001 a 9. júnom 2012 je 4166 dní / 365 = 11,41 roka.
Ak by bol úrok napr. 5 %, potom vieme, že:
- prvý vklad bude úročený po dobu 11,41 rokov, pri 5 %, t.j.:
BH = 1260 x [(1 + 0,05) na 11,41]
BH = 2199 €
- druhý vklad bude úročený po dobu 6,03 roku:
BH = 980 x [(1 + 0,05) na 6,03]
BH = 1315 €
- tretí vklad bude úročený 3,49 roku:
BH = 1780 x [(1 + 0,05) na 3,49]
BH = 2110 €
Spolu = 2199 + 1315 + 2110 = 5624 €
Do banky by ste vložili celkovo 4020 € a vybrali 5624 €. Zisk na úrokoch je 1604 €.
Výpočet úrokovej sadzby pri nepravidelných a nerovnomerných vkladoch.
S posledným uvedeným typom sporenia súvisí jeden zaujímavý problém – ako určiť výšku úrokovej sadzby, o ktorú sme zhodnotili naše peniaze, ak sme vkladali časovo nepravidelné alebo finančne nerovnomerné vklady.
Ak by boli vklady pravidelné – napr. vždy 15. dňa v mesiaci, a rovnomerné – napr. vždy po 100 Eur, určiť úrok by bolo pomerne jednoduché (MS Excel). Pri nepravidelných a nerovnomerných vkladoch však zlyháva aj ten.
Na ukážku použijeme predchádzajúci príklad, ktorý sme riešili. Budeme vedieť, kedy a koľko sme vkladali a tiež to, koľko máme dnes v banke našetrené (5624 €). Chceme vedieť, koľko nám naše vklady skutočne zarobili v percentách.
O našich doterajších vkladoch máme tieto informácie:
[1260 x [(1 + i) na 11,41]] + [980 x [(1 + i) na 6,03]] + [1780 x [(1 + i) na 3,49]] = 5624 €
i – (úroková miera) je v tomto prípade neznámou
všetky ostatné faktory sú pre nás známe – koľko sme vložili, ako dlho boli peniaze vložené, koľko je dnes našetrené.
Na to, aby sme vypočítali neznámu „i“, použijeme Excel.
- Do políčka A1 vložíme ľubovolnú úrokovú mieru – napr. 2 %. A1 sa bude ľahko pamätať, ako bunka, v ktorej hľadáme skutočný úrok, ktorý sme zarobili.
- Vedľa – do stĺpca B dáme pod seba jednotlivé vklady, v našom prípade
B1 = 1260 €
B2 = 980 €
B3 = 1780 €
- Do stĺpca C vložíme obdobie, počas ktorého sa budú jednotlivé vklady úročiť:
C1 = 11,41
C2 = 6,03
C3 = 3,49
- Do stĺpca D vložíme vzorec, ktorý je uvedený vyššie. Ten rozložíme na príslušný počet častí (v našom prípade 3). Stĺpec D bude teda vyzerať nasledovne:
D1 = 1260 x (1 + i) na 11,41
D2 = 980 x (1 + i) na 6,03
D3 = 1780 x (1 + i) na 3,49
Keďže my už máme uvedené hodnoty v Exceli napísané, môžeme ich do vzorca dosadiť. Neznámu „i“ nahradíme bunkou A1 (v tejto bunke budeme hľadať riešenie, zatiaľ sú tam 2 %). Vyzeralo by to nasledovne:
D1 = B1 x (1 + A1) na C1
D2 = B2 x (1 + A1) na C2
D3 = B3 x (1 + A1) na C3
Takto môžeme v Exceli vypočítať, koľko by sme dnes mali, keby sme vkladali konkrétne 3 sumy na daný počet rokov, pri predvolenej úrokovej miere 2 % (bunka A1). V tomto prípade by sme mali 4591 €. My ale vieme, že na účte je dnes 5624 €, t.j. podstatne viac.
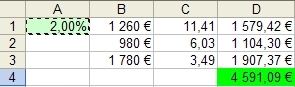
Prvým riešením je postupné ručné prepisovanie bunky A1 dovtedy, kým nám suma všetkých vkladov (D4) nebude dávať ich skutočnú súčasnú hodnotu 5624 €.
Druhou možnosťou je využiť v Exceli funkciu „hľadanie riešenia“. Nachádza sa pod záložkou Nástroje. Podstata tejto funkcie je v tom, že konkrétnu bunku prepisuje dovtedy, kým sa iná bunka nerovná nami definovanej konečnej hodnote. Funkcia vyžaduje určenie 3 parametrov. V našom prípade:
- nastaviť bunku: „D4“
skutočne našetrená suma všetkých vkladov, momentálne je tam pri úrokovej miere 2 % suma 4591 €
- cieľová hodnota: „5624“
pretože vieme, že je to suma, ktorú máme na účte a zarobili sme teda viac, ako zatiaľ uvedené 2 %
- menená hodnota: „A1“
percentá, ktoré bude Excel meniť dovtedy, kým sa bunka „D4“ nebude rovnať „5624“.

Stačí stlačiť tlačidlo OK a môžete sledovať, ako v priebehu sekundy Excel vypočíta, a do bunky A1 uvedie, správne riešenie. V našom prípade sa v bunke A1 ocitne hodnota 5 %. Pri 5 % sa totiž výsledná hodnota našich vkladov rovná presne 5624 Eurám, ktoré máme na účte dnes.
Následne sa s takýmto súborom môžete ľubovolne pohrať a sledovať, ako sa mení výška úrokovej sadzby, pri meniacej sa našetrenej sume. Ak by sme na našom účte mali momentálne napr. 10 000 €, vypočítame, že zhodnotenie vkladov, ktoré sme našimi investíciami dosiahli by bolo 13,20 %.
Excel umožňuje tieto výpočty ešte viac zjednodušiť – napr. nemusíme sami určiť, koľko rokov sa každý vklad bude individuálne úročiť, ale program sám dokáže vypočítať rozdiel medzi dátumom vkladu a dnešným (alebo ľubovolným iným) dátumom. To však už nie je priamo obsahom tohto článku. Cieľom bolo priniesť investorom riešenie základného problému – ako možno vypočítať skutočné zhodnotenie investovaných peňazí.
